Tom and Jerry is a combinatorics problem.

Problem

Here’s the link: https://open.kattis.com/problems/tomjerry

In this problem we are given a w by h grid and tasked to find the number of ways to get from the top left corner to the bottom right corner by only moving down or right. Furthermore, each valid path through the grid must pass through at least 1 of the given N points.

Approach

We solve some simpler problems and work the way up to a solution.

Remove valid path restriction

Consider the problem of finding the number of paths from top left to bottom right in a w by h grid. We know that any path from top left to bottom right must contain exactly w moves downward and exactly h moves to the right. Therefore, all valid paths are some permutation of the sequence of w down moves and h right moves. The number of these moves is nCr(w + h, w).

Number of valid paths that must pass through 1 given point

We can now consider the problem of finding the number of paths from top left to bottom right in a w by h grid that must pass through the point (x, y). Solving this is a direct extension from the previous problem. We know that any valid path from the top left corner to the bottom right corner must consist of two subpaths. Namely, the first is the path from the top left corner to the point (x, y). By the first problem the number of these points is nCr(x + y, x). In addition, the second path is the path from the point (x, y) to the point (w, h). There will be nCr(w + h, w) of these points. Since these two paths are independent of each other we can conclude that the number of paths satisfying this subproblem is the product of these combinations.

Number of valid paths that must pass through N given points

This is an induction on the previous problem. We can simply split the path into N + 1 subpaths, compute the number of possible paths for each subpath, and then multiply them all together. From this we can go on to solve the original problem.

Number of valid paths that pass through at least 1 of N given points

One idea for this problem is to enumerate every non-empty subset of the N points, check if it is a valid path, compute the number of paths for each one, and sum them all up. However, this will result in overcounting. For example, every path passing through (x, y) and (a, b) will also be considered when counting the paths through just (x, y). In order to fix this solution, we can use the inclusion-exclusion principle shown below.

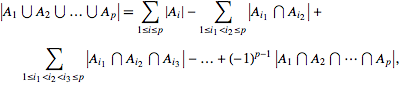
The simplest case of the this principle can be seen when N = 2. Consider the venn diagram below.

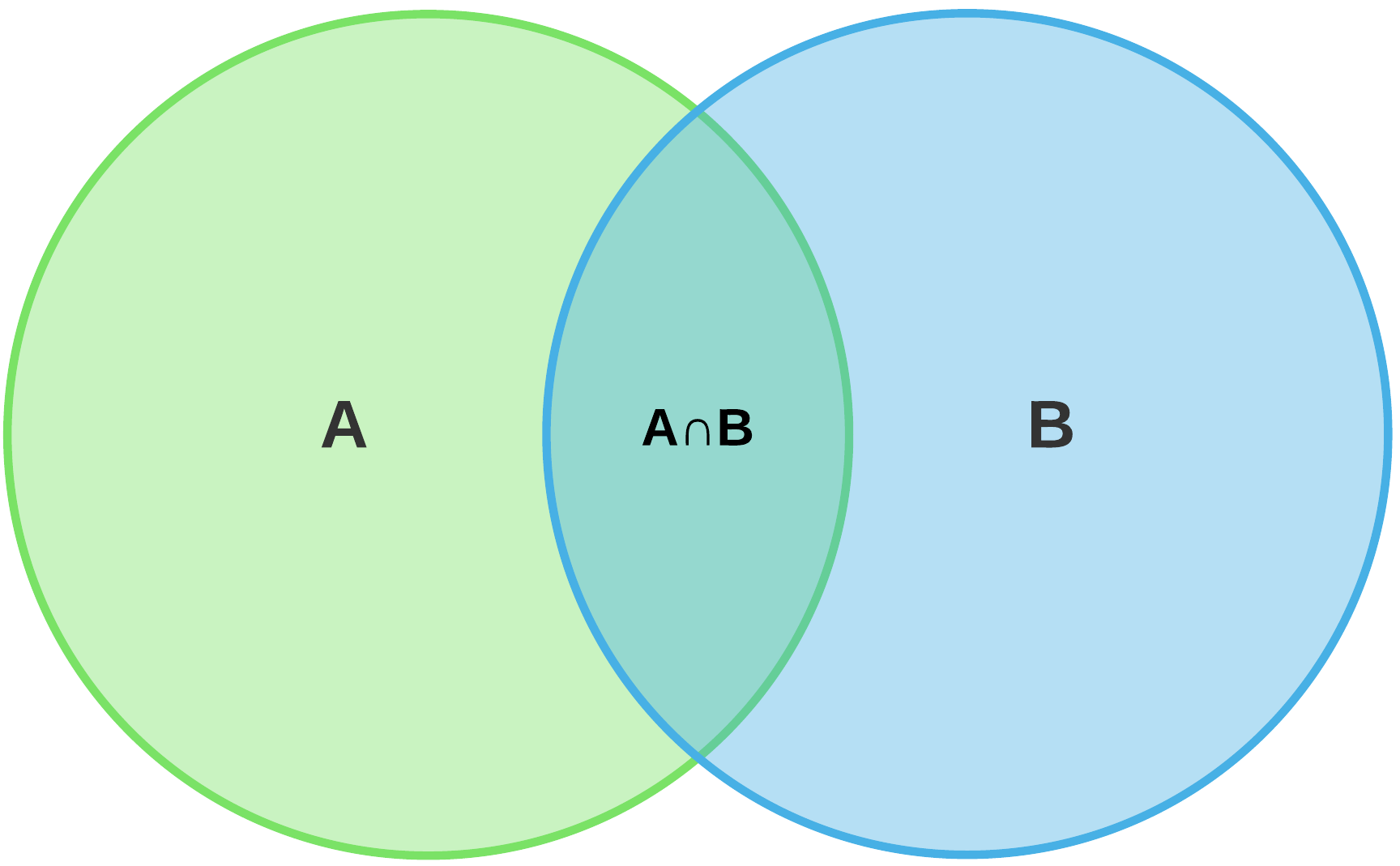
The total set of elements in the set A U B is A + B - A ^ B. We must subtract the intersection of the two sets because otherwise we would count it twice as seen in the Venn diagram. From this, the inclusion-exclusion principle can by derived by inducting on N.

Let the set of valid paths that pass through at least 1 of N given points be A. This set is equal to the union of {A1, A2, …, AN} where Ai is the set of valid paths that pass through point i. We can compute this set using the inclusion-exclusion principle. Each subproblem in this computation is an instantiation of the simpler problem provided above.

Code

As routine, we precompute our factorials and define some useful helper functions.

const llint MOD = 1000000007;
const llint MAXN = 200001;

llint fact[MAXN];

void setup() {
    fact[0] = 1;
    for(int i = 1; i < MAXN; i++) {
        fact[i] = i * fact[i - 1] % MOD;
    }
}

llint pow(llint base, llint exp) {
    llint res = 1;
    llint basePower = base;
    for(llint k = 1; k <= exp; k <<= 1) {
        if((k & exp) > 0) {
            res = (res * basePower) % MOD;
        }
        basePower = (basePower * basePower) % MOD;
    }
    return res;
}

inline llint inv(llint x) {
    return pow(x, MOD - 2);
}

llint nCr(llint a, llint b) {
    return (((fact[a] * inv(fact[b])) % MOD) * inv(fact[a - b])) % MOD;
}

We can define a struct representing a point on the board with an overrided comparator to make life easier. Note that some combinations of points may not be valid. For example there are no paths passing through both the points (1, 2) and (2, 1) on any grid because going from any one to the other will require a move in either the up or left direction. We can check for these cases with the valid() function.

Finally, we can define a paths() function that actually computes the number of paths for a given sequence of points. The code follows from the results of the easier problems in the approach section.

struct pos {
    int x;
    int y;
    pos(int xx, int yy) {
        x = xx;
        y = yy;
    }
    bool operator<(const pos& o) {
        return not(o.x < x or (o.x == x and o.y < y));
    }
};

bool valid(vector<pos>& p) {
    for(int i = 0; i < p.size() - 1; i++) {
        pos a = p[i];
        pos b = p[i + 1];
        if(a.x > b.x or a.y > b.y) {
            return false;
        }
    }
    return true;
}

llint paths(vector<pos>& cheeses, int w, int h) {
    llint res = 1;
    pos prev(1, 1);
    for(pos& p : cheeses) {
        int nx = p.x - prev.x;
        int ny = p.y - prev.y;
        res *= nCr(nx + ny, nx);
        res %= MOD;
        prev = p;
    }
    int nx = w - prev.x;
    int ny = h - prev.y;
    res *= nCr(nx + ny, nx);
    res %= MOD;
    return res;
}

Finally, we need a way to generate all subsets of the set of N points in order to compute the subproblems needed for the inclusion-exclusion principle. We can define a subsets(vv, cur, p, index, size) function that places all subsets of p of size size into the collection vv.

void subsets(vector<vector<pos>>& vv, vector<pos> cur, vector<pos> p, int index, int size) {
    if(size == 0) {
        vv.push_back(vector<pos>(cur));
        return;
    }
    for(int i = index; i < p.size(); i++) {
        cur.push_back(p[i]);
        subsets(vv, vector<pos>(cur), p, i + 1, size - 1);
        cur.pop_back();
    }
}

We can combine all this to get an answer.

int main() {
    setup();
    int w, h, n;
    cin >> w >> h;
    cin >> n;
    vector<pos> cheeses;
    for(int i = 0; i < n; i++) {
        int x, y;
        cin >> x >> y;
        cheeses.push_back(pos(x, y));
    }
    sort(cheeses.begin(), cheeses.end());
    llint res = 0;
    llint mult = -1;
    for(int i = 1; i <= n; i++) {
        mult *= -1;
        vector<vector<pos>> vv;
        subsets(vv, vector<pos>(), cheeses, 0, i);
        for(auto v: vv) {
            if(valid(v))  {
                llint cur = mult * paths(v, w, h);
                cur = (cur + MOD) % MOD;
                res += cur;
                res %= MOD;
            }
        }
    }
    cout << res << endl;
    return 0;
}